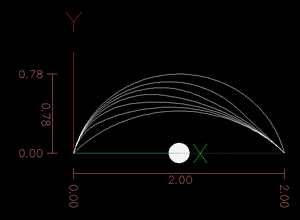
A biarc consists of two arcs which are tangent where they meet. By defining the initial and final locations, and the initial and final tangents, you're one number short of determining a unique biarc. The remaining parameter "r" (or α/β) determines where the split is between the first and second arc.
A great many of the papers on curve fitting with biarcs seem to be concerned with how to choose the remaining parameter to minimize error. However, based on the figures in the paper "Optimal Single Biarc Fitting and its Applications", it looks like the simple method "r=1" may be best suited to emc's trajectory planner: emc begins to behave poorly as segments get shorter. "r=1" appears to generate biarcs with similar average length, while the "Optimal" method proposed in that paper generates biarcs of wildly varying length.
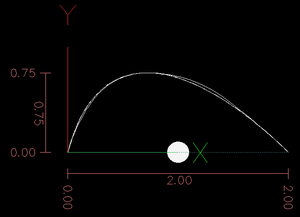
The results from this program mirror those of my earlier arc-to-bezier fitting program: With even a small number of arcs, the fit becomes very good.
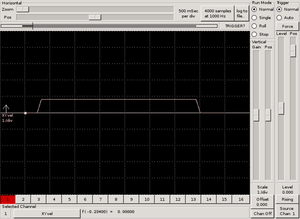
I completed the spline shown above into a closed loop with C1 continuity at the joins. The velocity profile (which includes 3 runs with different numbers of biarcs) is quite good, which shows the pleasing results the emc trajectory planner has as long as acceleration is reasonable and the primitives are not too short.
Updated 2007/11/23: I updated the image to show EMC 2.2's even better velocity profile. I updated biarc.py to have GPL copyright block.
Updated 2007/12/18: I found this paper helpful in understanding the biarc math. I only read the paper as far as Fig 1 and the associated math, ignoring most of the rest.
Files currently attached to this page:
(originally posted on the AXIS blog)
Entry first conceived on 18 February 2007, 3:06 UTC, last modified on 15 January 2012, 3:46 UTC
Website Copyright © 2004-2024 Jeff Epler