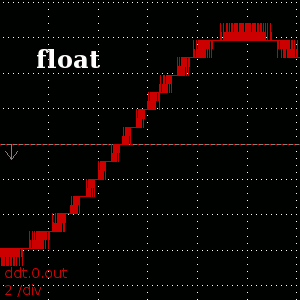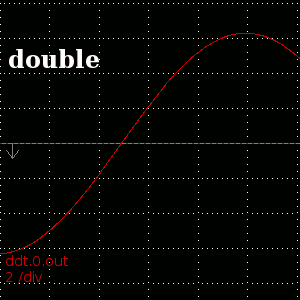
Result of 'ddt' of sin(t)+10000 showing the difference that 'double' precision makes
After reading the source to current versions of gcc, and thinking about the motivations for writing "two movl" sequences to load or store doubles on x86, I have a high level of confidence that the guarantee on Pentiums for 8-byte-aligned doubles is enough to give the same atomicity requirements for 'double' pins as other types, as long as a few assumptions are made about the compiler. I've produced a patch and show one way in which this is a big improvement.
Motivation
One place where more precise representation of real numbers helps is in the numeric computation of derivatives. The naive formula for the derivative of f(t) near t=t0 is (f(t0) - f(t0-epsilon)) / t0. This formulation includes the subtraction of two nearly-equal values, a very bad case for finite-precision arithmetic. As the function gets further and further from the origin, the result of this subtraction has fewer and fewer significant digits, leading to the ugly aliased result. With doubles, the distance at which this starts to occur is pushed much further away, so that there is an immediately visible difference in the numeric derivative ofThere are many other places in emc where more precision would be nice. The same precision problems exist, for instance, when determining following error on axis positions which reach into the 10000s or 100000s---think rotary axes which almost always turn in one direction, frequently seen when using cnc to create gears.
Is it possible?
Recall that HAL works on the principle that updates to all values must be atomic, and currently all assignments to HAL pins are of the simple form*pin is therefore restricted to types for which gcc always generates atomic store operations.*pin = newvalue;
On Pentium systems, 8-byte-aligned 8-byte stores (such as with the fld and fst instructions) give the same guarantees as 4-byte-aligned 4-byte stores (such as movl).
Historically, two main problems that I am aware of prevented us from taking advantage of this property. First, when hal was conceived, it was pretty reasonable to imagine it running on pre-Pentium systems where there is no atomicity guarantee for fld/fst. Second, it was poorly understood when gcc would generate fld/fst, and when it might produce some other sequence such as the "two movl" sequence.
In 2008, we are promoting Pentium-III PCs as minimum for emc (in part because this performance level is needed for gnome and for emc's modern GUIs, and in part because almost everyone is using systems with this performance level anyway). Since 2006 or so we have required that systems include the 'rdtsc' instruction, and have never heard from anyone who couldn't use emc because of this detail. We can depend on Pentium-class CPUs.
I have also recently spent time looking at what current gcc does to load and store floats. While I can't say with certainty what it does in all cases (and I certainly can't say for sure what future versions of gcc will do), I believe I understand where and why it chooses to use "two movl" sequences---and, more importantly, I am pretty sure I know how to prevent it from doing so, and instead giving fld/fst in all the cases I looked at.
Basically, gcc in any optimizing mode will attempt to generate an instruction sequence that is fairly efficient. This leads to guess that if any arithmetic is done on a floating-point value, it will be loaded from memory using fld, and the result will be stored with fst. The alternative would be to store it in a temporary location, then move it from the temporary location to the final location with the "two movl" sequence, which is so obviously suboptimal that I just can't believe gcc ever does it.
That leaves two basic cases to look at: direct memory-memory assignments (like the *pin = newvalue; example) and constant memory assignments (*pin = 1.0).
(Actually, a third one occurs to me: you might think to write *pin = -newvalue; as an integer operation, since it is merely inverting the top bit; a similar argument can be made for abs. I can't find any sign that gcc actually does this, though.)
What were they thinking?
Let's take a moment to consider the lowly 486. This system has a 32-bit memory interface, so "fst" and "two movl" will both perform about the same in terms of number of memory accesses. But maybe our code will be running on a 486SX which lacks a floating-point coprocessor. In that case, it would be a nice performance improvement to avoid trapping into the floating point emulator just to store a floating-point number. That's where the "two movl" sequence pays off in a big way--on a class of machine I probably haven't used in the last 15 years. (comments in other machine description files in gcc lead me to believe that until the Pentium4 there may have still been a slight performance penalty for fld/fst compared to two moves:;; Moves usually have one cycle penalty, but there are exceptions. (define_insn_reservation "pent_fmov" 1
In the gcc i386.md file, there are several alternatives for "movdf" (move double-precision float). One of them is called "movdf_integer", and it is deactivated by (among other conditions) (optimize_size || !TARGET_INTEGER_DFMODE_MOVES). This ties in exactly with the methods I found for avoiding the "two movl" sequence: either specifiy a modern architecture with -mtune=pentium4, or specify space optimization with -Os. (fld/fst is certainly a shorter sequence than movl/movl/movl/movl!)
Double Down
It is the latter (Optimize -Os) that I have chosen to do. -Os may have a beneficial effect on emc, aside from this issue: reducing i-cache misses by reducing code size. (i-cache misses contribute to total time in hal threads, and particularly to spiky time values) Of course, doubling the size and alignment of the most common hal data type will increase data size, so I have no illusions that it will be better than a wash.This required a fair number of other changes--in some places, temporaries of type "float" were deliberately used. In other places, the assumption was made that sizeof(hal_float) == sizeof(hal_s32). Overall, I was a little surprised at the size of the patch. However, the testsuite works, emc works, and halscope works. I haven't actually run any torture tests designed to determine whether these stores really are atomic, though.
I'd be thrilled if this could get into emc 2.3, but for now I'm going to let it live as a patch.
$ diffstat doubles.patch Makefile | 2 +- hal/components/ddt.comp | 4 ++-- hal/components/pid.c | 8 ++++---- hal/components/streamer.h | 4 ++-- hal/hal.h | 4 +++- hal/hal_lib.c | 30 +++++++++++++++++++++++------- hal/hal_priv.h | 12 +++++++++++- hal/utils/halcmd_commands.c | 2 +- hal/utils/scope_disp.c | 4 ++-- hal/utils/scope_files.c | 2 +- hal/utils/scope_rt.c | 22 ++++++++++++++-------- hal/utils/scope_shm.h | 5 +++-- hal/utils/scope_trig.c | 4 ++-- 13 files changed, 69 insertions(+), 34 deletions(-)
Files currently attached to this page:
| doubles.patch | 14.5kB |
(originally posted on the AXIS blog)
Entry first conceived on 31 October 2008, 21:04 UTC, last modified on 15 January 2012, 3:46 UTC
Website Copyright © 2004-2024 Jeff Epler