Cancellation error

I was recently reminded of the importance of choosing numeric algorithms that don't behave catastrophically for certain inputs. One example is the calculation of 1-cos(θ) for small θ. In this case, cos(θ) is very close to 1, leading to a large cancellation error in the subtraction step.

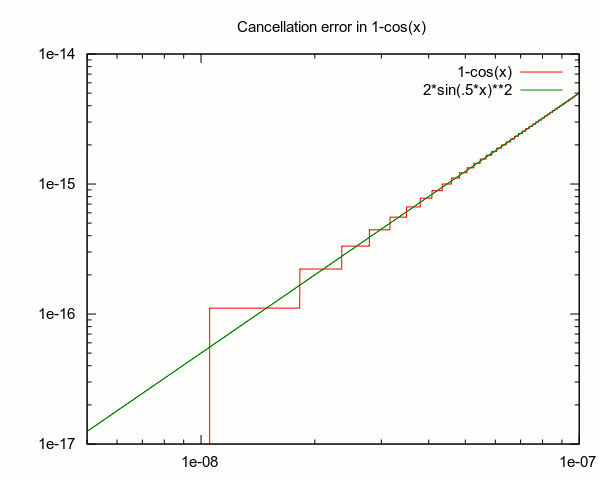
What is to be done about this? Seek out an equivalent expression that does not suffer from cancellation error. In this case, employ the double-angle formula cos(2u) = 1-2sin²(u). This yields the equivalent expression 2sin(θ/2)², which gives good numeric results for θ close to zero.

This plot shows how the accuracy of the original formula starts to visibly degrade at around 1e-7 and gets steadily worse until, at about 1e-8, it actually drops to 0.

I wonder whether it would be useful to have a valgrind-like tool warn when disastrous cancellation occurs, or whether typical programs would have way too many such errors to ever contemplate fixing them all…

Entry first conceived on 7 March 2012, 15:42 UTC, last modified on 7 March 2012, 16:02 UTC
Website Copyright © 2004-2024 Jeff Epler