Here's a small snippet for setting a local coordinate system. You need to know the location to treat as origin as well as the direction vectors to treat as X and Y.
// Take a position vector (p) and 3 direction vectors (uvw)
// and create a transformation matrix. The origin is transformed to p,
// and xyz point along uvw.
// Normally, the caller will ensure that uvw are orthogonal unit vectors
function puvw(p, u, v, w) = [
[u[0], v[0], w[0], p[0]],
[u[1], v[1], w[1], p[1]],
[u[2], v[2], w[2], p[2]]];
// Take a position vector (p) and 2 direction vectors (uv) which should be
// orthogonal but need not be unit vectors. Calculate the unit vectors as well
// as the third vector and return the resulting matrix
function puv(p, u, v) =
let(nu = u / norm(u), nv = v / norm(v), nw = cross(nu, nv))
puvw(p, nu, nv, nw);
// Operate in a local coordinate system where the origin is the point p,
// x points along u, y points along v, and z points along the normal vector
// to uv. x and y should be orthogonal but need not be unit vectors.
module puv(p, u, v) {
multmatrix(puv(p, u, v)) children();
}
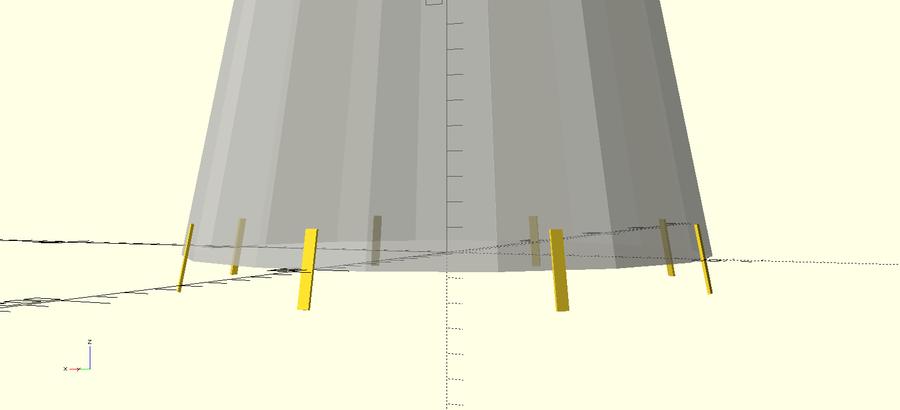
For instance, suppose you want to lay out some feature relative to a cone 100mm in diameter and 500mm tall. It's convenient to set the origin to the intersection of the cone base with the +x axis, +x be the direction from the base of the cone to the tip, +y be the direction tangential to the cone, and +z be the direction 'out' from the cone. You might invoke puv like so (corr is a factor to make the flats of the faceted cone exactly touch the 100mm diameter circle):
effen = 16; // 16, 32, 64, ... corr = 1 / cos(180/effen); for(i=[0:45:360]) rotate(i) puv([100,0,0], [-100, 0, 500], [0, -1, 0]) linear_extrude(height=1) square([25, 4], center=true); %rotate(45/4) cylinder(d1=200*corr, d2=0, h=500, $fn=effen);
Entry first conceived on 7 November 2022, 1:35 UTC, last modified on 7 November 2022, 1:52 UTC
Website Copyright © 2004-2024 Jeff Epler